凯利公式是什么 为什么说凯利公式是神奇的财富公式

　　凯利公式最初为AT&T贝尔实验室物理学家约翰·拉里·凯利根据他的同僚克劳德·艾尔伍德·夏农于长途电话线杂讯上的研究所建立。凯利解决了夏农的资讯理论要如何应用于一名拥有内线消息的赌徒在赌博时的问题。赌徒希望决定最佳的赌注金额，而他的内线消息不需完美（无杂讯），即可让他拥有有用的优势。凯利的公式随后被夏农的另一名同僚爱德华·索普应用于二十一点和股票市场中。

　　索普利用工作之余，通过数个月的艰苦演算，写了一篇题为《“二十一点”优选策略》的数学论文。他利用自己的知识，一夜之间“奇袭”了内华达雷诺市所有的赌场，并成功的从二十一点赌桌上赢得了上万美元。他还是美国华尔街量化交易对冲基金的鼻祖，70年代首创第一个量化交易对冲基金。1962年出版了他的专著《打败庄家》，成为金融学的经典著作之一。

　　凯利公式是什么

　　凯利公式是一个在高级赌徒的世界里大名鼎鼎，是顶级高手常用的数学利器。那什么是凯利公式？我们先看一个例子。

　　一个1赔2（不包括本金）的简单赌局，扔硬币下注，假设赌注为1元，硬币如果为正面则净赢2元，如果为反面则输掉1元。现在你的总资产为100元，每一次的押注都可投入任意金额。

　　你会怎么赌呢？已知掷硬币后正反面的概率都为50%，赔率是1赔2（不包括本金），那么这个赌局你只要不断地下注，再抛开不公平因素的干扰，几乎就能赚。

　　因为掷硬币次数越多，其正反面出现概率就越会稳定在50%，收益2倍，损失却只是1倍，从数学上讲那是稳赚不赔的赌局。

　　但实际情况却可能会有偏差。

　　如果你是冒险主义者，你可能会想，要玩就玩大的，一次性把100元全押上，幸运的话，一次正面就可以获得200元，又是一段值得炫耀的赌史。可是，如果输了，得把100元资产拱手献给对方，你就一无所有。好不容易来趟拉斯维加斯，这肯定不是明策。

　　如果你是保守主义者，你可能会想，谨慎一些，慢慢来。你每次只下注1元，正面赢2元，反面输1元。玩了20把突然觉得，对方下注10元一次就赢得20元，自己一次才赢2元、10次才能赢得20元，感觉自己已经错过几个亿而开始后悔！

　　那到底该以多少比例下注才能获得最大收益呢？普通赌徒一般一脸茫然，但凯利公式却能够告诉我们答案：

　　每次下注比例为当时总资金的25%，这样就能获得最大收益。

　　为什么说凯利公式是神奇的财富公式

　　让我们来看看凯利公式的庐山真面目：

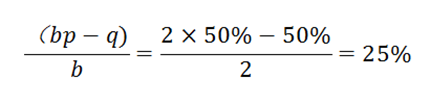
　　式中，各参数意义为：

　　f为应投注的资本比例；

　　p为获胜的概率（抛到硬币正面的概率）；

　　q为失败的概率，即（抛到硬币反面的概率）；

　　b为赔率，等于期望盈利÷可能亏损（盈亏比）；

　　公式上面的分子(bp-q)代表“赢面”，数学中叫“期望值”。

　　什么才是不多不少的赌注呢？凯利告诉我们要通过选择最佳投注比例，才能长期获得最高盈利。

　　回到前面提到的例子中，硬币抛出正、反面的概率都是50%，所以p、q（获胜、失败的概率）都为0.5，而赔率＝期望盈利÷可能亏损=2元÷1元，赔率就是2，也就是说这个赌局次数越多，我们收益就越高。

　　那么如何利用手中的资金来获得最高收益呢，我们要求的答案是f，也就是

　　由此，我们根据凯利公式的计算而得投注比例，每次都拿出当前手中资金的25%来进行下注。设初始资金为100，硬币为正面时，收益为投注的2倍，为反面则失去投注金额。在下表中，我们模拟计算了10次赌局的收益情况。

　　25%投注下10次收益表-1

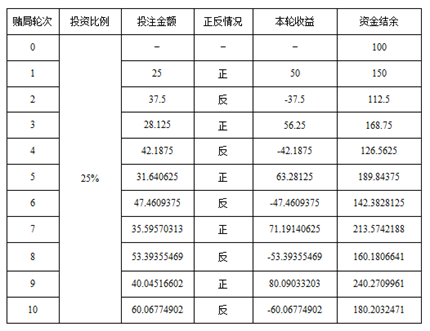
　　25%投注下10次收益表-2

　　图-1中从先正后反的情况计算了收益，而图-2则计算了正反分布交错情况下的收益结果。

　　比较两表，我们最终可以发现其收益是相等的，硬币出现正反面的先后顺序对于最终收益的计算结果并无影响。

　　而按25%的投注比例进行投注，收益基本呈现稳步增长的大趋势。

　　但假设投注比例为100%时，10次当中只要出现任意一次的反面，就会彻底输光身上的所有钱，直接出局，且每轮反面概率还为50%；

　　而每次投注1元，即投注比例为1%的时候，10次数学上的收益为，这风险很小，但收益太低。由此看来，凯利公式才是最大的赢家。

　　赌场操盘者每一次下注的时候，都会谨记数学原则；而作为普通赌徒，除了心中默念“菩萨保佑”外，哪里知道这后面的数学知识？

　　所以，就算你赢得了“财神爷”的支持，也永远赢不了“凯利公式”。